GCD(最大公约数) #
这里就不说GCD的定义,讲一些性质:
-
最小公倍数求法: \(lcm(a,b) = \frac{ab}{gcd(a,b)}\)
-
区间的最大公约数
$$ Def. \quad GCD_{i=l}^{r} P_i= gcd(P_l, GCD_{i=l+1}^{r} P_i) \quad i.e. GCD_{i=r}^{r} P_i = P_r $$表示区间\([l,r]\)中所有数的最大公约数。有如下性质:
- \( \forall k, s.t. k \in N, l \leq k \leq r, \quad GCD_{i=l}^{r} P_i = gcd(GCD_{i=l}^{k} P_i, GCD_{i=k+1}^{r} P_i)\) 这个性质可以用在线段树,ST表存储区间GCD。区间和、最大、最小值也有这样的性质
- \( \forall r_1,r_2, s.t. r_1,r_2 \in N, l \leq r_1 \leq r_2, \quad GCD_{i=l}^{r_1} P_i \geq GCD_{i=l}^{r_2} P_i \) 这个性质常常用来区间二分。区间和、最大、最小值也有类似的性质,注意其中有的运算(和、最大值)要把不等号取反。
-
裴蜀定理
- 对于正整数\(a,b\)存在整数\(x,y\)使得\(gcd(a,b)=ax+by\)。
- 整数\(a,b\)互质的充要条件是存在整数\(x,y\)使得\(ax+by=1\)。
- \(ax+by\)必定是\(gcd(a,b)\)的整数倍。
- 运用范围:数论问题求解;在长度为\(n\)的循环链表中进行定长为\(k\)的跳跃等。
异或 #
定义 #
在逻辑学中,逻辑算符异或(exclusive or)是对两个运算元的一种逻辑析取类型,符号为 \(XOR\) 或 \(EOR\) 或 \(\oplus\)(编程语言中常用^)。但与一般的逻辑或不同,异或算符的值为真仅当两个运算元中恰有一个的值为真,而另外一个的值为非真。转化为命题,就是:“两者的值不同。”或“有且仅有一个为真。”
\(0 \oplus 0 = 0\)
\(0 \oplus 1 = 1\)
\(1 \oplus 0 = 1\)
\(1 \oplus 1 = 0\)
性质 #
-
交换律:\(A \oplus B = B \oplus A\)
-
结合律:\(A \oplus (B \oplus C) = (A \oplus B) \oplus C\)
-
自反性:\(A \oplus A = 0\)。任何数与自身异或的结果都是0。
-
恒等律:\(A \oplus 0 = A\)。任何数与0异或的结果都是其自身。
-
逆元:\( A \oplus B = C\),则 \( C \oplus B = A\) 。可以用来“撤销”或“还原”之前的异或操作。
-
多次异或同一个数:对一个数进行偶数次异或操作结果不变,奇数次异或操作等于异或该数一次。
\(e.g.\)
- 偶数次:\(A \oplus A \oplus A = A \);
- 奇数次:\(A \oplus A \oplus A \oplus A = A \oplus A = 0\);
\(Co.\) 每进行一次异或操作,就相当于对当前的 1 的个数的奇偶性进行一次翻转。可以利用这一性质对区间中奇数个数的奇偶性判断。
- \(\bigoplus_{i = l} ^ {r} P[i] \) 是奇数 \( \iff P[l \sim r]\) 有奇数个奇数。
- \(\bigoplus_{i = l} ^ {r} P[i] \) 是偶数 \( \iff P[l \sim r]\) 有偶数(包括0)个奇数。
-
区间异或和 可以通过预处理区间的前缀异或和,即\(pre[i] = P[1] \oplus P[2] \oplus \cdots \oplus P[i]\),由第五点性质得区间\([l,r]\)的异或和: \(\bigoplus_{i = l} ^ {r} P[i] = P[l] \oplus P[l+1] \oplus \cdots P[r-1] \oplus P[r] = pre[r] \oplus pre[l−1]\)。
贪心方法证明——交换法 #
贪心的交换论证思路 #
- 假设先选\(i\)再选\(j\);
- 假设上述选法是对的,先选\(i\)再选\(j\)的代价小于先选\(j\)再选\(i\),即满足\(f(i,j) < f(j,i)\)(贡献等可反之,具体分析);
- 化简\(f(i,j) < f(j,i)\),得到满足的条件。根据条件进行排序计算。
例题和解析 #
GDCPC2024 C #
题意:给一棵以1为根的树,每个点有权值\(w_i\),找最优的dfs序(遍历子节点的顺序),求\( max(\sum {p_i} {w_i}) \),其中\(p\)为dfs序。
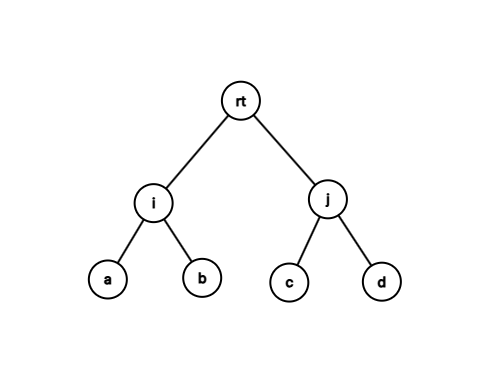
如下图,当前根为\(rt\),假设dfs时“以\(i\)为根的子树后选,以\(j\)为根的子树先选”是最优的顺序,则有贡献\( (siz[rt]−1−siz[i])∗f[i]+(siz[rt]−1−siz[i]−siz[j])∗f[j] \),其中\(siz\)表示子树大小,\(f\)表示子树权值和。
交换一下顺序,若先选\(i\)再选\(j\),则有贡献\( (siz[rt]−1−siz[j])∗f[j]+(siz[rt]−1−siz[j]−siz[i])∗f[i] \),展开后发现不同项为\( −siz[i]∗f[j]>−siz[j]∗f[i]\),即\(\frac{siz[i]}{f[i]}<\frac{siz[j]}{f[j]} \),按照这个顺序选择子树即可。